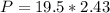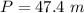Answer:
The position is
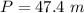 relative to the base of the ocean
relative to the base of the ocean
Step-by-step explanation:
From the question we are told that
The angle made by the incline with the horizontal is
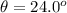
The constant acceleration is

The distance covered is
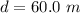
The height of the cliff is
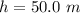
The velocity of the car is mathematically represented as

The initial velocity of the car is u= 0
So
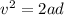
substituting values
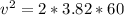
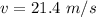
The vertical component of this velocity is
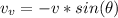
substituting values
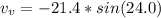

The negative sign is because is moving in the negative direction of the y-axis
The horizontal component of this velocity is
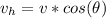
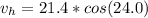
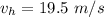
Now according to equation of motion we have
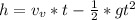
substituting values
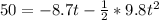
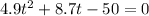
using quadratic equation we have that
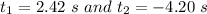
given that time cannot be negative

The car’s position relative to the base of the cliff when the car lands in the ocean is mathematically evaluate as
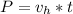
substituting values