Answer:
158.13m
Step-by-step explanation:
Force exerted over a unit area is called Pressure. Also, in a given column of air, the pressure(P) is given as the product of the density(ρ) of the air, the height(h) of the column of air and the acceleration due to gravity(g). i.e
P = ρhg
Let;
Pressure measured at the roof top = (
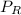 )
)
Pressure measured at the ground level = (
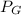 )
)
Pressure at the ground level = Pressure at the roof + Pressure at the column height of air.
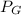 =
=
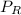 + P ---------------(i)
+ P ---------------(i)
(a) P = ρhg -----------(***)
But;
ρ = density of air = 1.29kg/m³
h = height of column of air = height of building
g = acceleration due to gravity = 10m/s²
Substitute these values into equation (***)
P = 1.29 x h x 10
P = 12.9h Pa
(b)
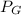 = ρ
= ρ
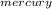 x h
x h
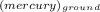 x g ------------(*)
x g ------------(*)
But;
ρ
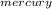 = density of mercury = 13600kg/m³
= density of mercury = 13600kg/m³
h
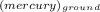 = height of mercury on the ground = 760.0mm = 0.76m
= height of mercury on the ground = 760.0mm = 0.76m
g = acceleration due to gravity = 10m/s²
Substitute these values into equation (*)
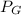 = 13600 x 0.76 x 10
= 13600 x 0.76 x 10
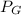 = 103360 Pa
= 103360 Pa
(c)
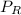 = ρ
= ρ
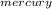 x h
x h
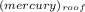 x g --------------(**)
x g --------------(**)
But;
ρ
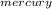 = density of mercury = 13600kg/m³
= density of mercury = 13600kg/m³
h
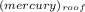 = height of mercury on the roof = 745.0mm = 0.745m
= height of mercury on the roof = 745.0mm = 0.745m
g = acceleration due to gravity = 10m/s²
Substitute these values into equation (**)
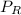 = 13600 x 0.745 x 10
= 13600 x 0.745 x 10
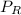 = 101320 Pa
= 101320 Pa
(d) Now that we know the values of P,
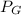 and
and
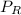 , let's substitute them into equation (i) as follows;
, let's substitute them into equation (i) as follows;
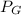 =
=
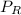 + P
+ P
103360 = 101320 + 12.9h
Solve for h;
12.9h = 103360 - 101320
12.9h = 2040
h =
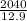
h = 158.13m
Therefore, the height of the building is 158.13m