Question

According to the National Association of Theater Owners, the average price for a movie in the United States in 2012 was $7.96. Assume the population standard deviation is $0.50 and that a sample of 30 theaters was randomly selected.

Required:
a. Calculate the standard error of the mean.
b. What is the probability that the sample mean will be less than $7.75?
c. What is the probability that the sample mean will be less than $8.10?
d. What is the probability that the sample mean will be more than $8.20?

Answer 1

(a) The standard error of the mean is 0.091.

(b) The probability that the sample mean will be less than $7.75 is 0.0107.

(c) The probability that the sample mean will be less than $8.10 is 0.9369.

(d) The probability that the sample mean will be more than $8.20 is 0.0043.

Explanation:

We are given that the average price for a movie in the United States in 2012 was $7.96.

Assume the population standard deviation is $0.50 and that a sample of 30 theaters was randomly selected.

Let
`\bar X` = sample mean price for a movie in the United States

The z-score probability distribution for the sample mean is given by;

Z =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean price for a movie = $7.96

`\sigma` = population standard deviation = $0.50

n = sample of theaters = 30

(a) The standard error of the mean is given by;

Standard error =
`(\sigma)/(√(n) )` =
`(0.50)/(√(30) )`

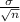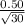
= 0.091

(b) The probability that the sample mean will be less than $7.75 is given by = P(
`\bar X` < $7.75)

P(
`\bar X` < $7.75) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` <
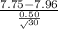`\frac{7.75-7.96}{\frac{0.50}√(30) } }` ) = P(Z < -2.30) = 1 - P(Z
`\leq` 2.30)

= 1 - 0.9893 = 0.0107

The above probability is calculated by looking at the value of x = 2.30 in the z table which has an area of 0.9893.

(c) The probability that the sample mean will be less than $8.10 is given by = P(
`\bar X` < $8.10)

P(
`\bar X` < $8.10) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` <
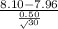`\frac{8.10-7.96}{\frac{0.50}√(30) } }` ) = P(Z < 1.53) = 0.9369

The above probability is calculated by looking at the value of x = 1.53 in the z table which has an area of 0.9369.

(d) The probability that the sample mean will be more than $8.20 is given by = P(
`\bar X` > $8.20)

P(
`\bar X` > $8.20) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` >
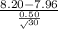`\frac{8.20-7.96}{\frac{0.50}√(30) } }` ) = P(Z > 2.63) = 1 - P(Z
`\leq` 2.63)

= 1 - 0.9957 = 0.0043

The above probability is calculated by looking at the value of x = 2.63 in the z table which has an area of 0.9957.