Question

A survey collects demographic, socioeconomic, dietary, and health-related information on an annual basis. Here is a sample of 20 observations on HDL cholesterol level (mg/dl) obtained from the survey (HDL is "good" cholesterol; the higher its value, the lower the risk for heart disease):

35 49 51 54 65 51 52
47 87 37 46 33 39 44
39 64 94 34 30 48

Requried:
a. Calculate a point estimate of the population mean HDL cholesterol level.
b. Making no assumptions about the shape of the population distribution, calculate a point estimate of the value that separates the largest 50% of HDL levels from the smallest 50%.
c. Calculate a point estimate of the population standard deviation.

Answer 1

(a) The point estimate of the population mean HDL cholesterol level is 49.95.

(b) The point estimate of the value that separates the largest 50% of HDL levels from the smallest 50% is 47.5.

(c) The point estimate of the population standard deviation is 16.85.

Explanation:

We are given a sample of 20 observations on HDL cholesterol level (mg/dl) obtained from the survey below;

35, 49, 51, 54, 65, 51, 52, 47, 87, 37, 46, 33, 39, 44, 39, 64, 94, 34, 30, 48.

(a) The point estimate of the population mean HDL cholesterol level is given by the sample mean of the above data, i.e;

Sample Mean,
`\bar X` =
`(\sum X)/(n)`

=
`(35+ 49+ 51+ 54 +65 +51+ 52+ 47+ 87+ 37+ 46+ 33+ 39+ 44+ 39+ 64+ 94+ 34+ 30+ 48)/(20)`

=
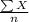
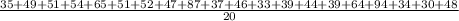
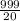`(999)/(20)` = 49.95

So, the point estimate of the population mean HDL cholesterol level is 49.95.

(b) The point estimate of the value that separates the largest 50% of HDL levels from the smallest 50% is given by the Median of the above data.

Firstly, arranging the given data in ascending order we get;

30, 33, 34, 35, 37, 39, 39, 44, 46, 47, 48, 49, 51, 51, 52, 54, 64, 65, 87, 94.

Now, for calculating median we have to first observe that the number of observations (n) in our data is even or odd, i.e;

• If n is odd, then the formula for calculating median is given by;

Median =
`((n+1)/(2))^(th) \text{ obs.}`

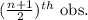
• If n is even, then the formula for calculating median is given by;

Median =
`\frac{((n)/(2))^(th) \text{ obs.}+((n)/(2)+1)^(th) \text{ obs.} }{2}`

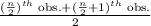
Here, the number of observations is even, i.e. n = 20.

So, Median =
`\frac{((n)/(2))^(th) \text{ obs.}+((n)/(2)+1)^(th) \text{ obs.} }{2}`

=
`\frac{((20)/(2))^(th) \text{ obs.}+((20)/(2)+1)^(th) \text{ obs.} }{2}`

=
`\frac{(10)^(th) \text{ obs.}+(11)^(th) \text{ obs.} }{2}`

=
`(47+48 )/(2)`

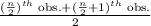
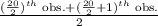
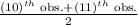
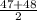
Median = 47.5

Hence, the point estimate of the value that separates the largest 50% of HDL levels from the smallest 50% is 47.5.

(c) The point estimate of the population standard deviation is given by the following formula;

Standard deviation, s =
`\sqrt{(\sum(X-\bar X)^(2) )/(n-1) }`

=
`\sqrt{\frac{ (30-49.95)^(2)+(33-49.95)^(2)+(34-49.95)^(2)+........+(94-49.95)^(2)}{{20-1}} }} }`

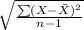
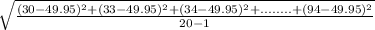
= 16.85