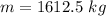Question

A large grinding wheel in the shape of a solid cylinder of radius 0.330 m is free to rotate on a frictionless, vertical axle. A constant tangential force of 250 N applied to its edge causes the wheel to have an angular acceleration of 0.940 rad/s2. What is the mass of the wheel?

Answer 1

The mass of the solid cylinder is
`m = 1612.5 \ kg`

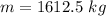
Step-by-step explanation:

From the question we are told that

The radius of the grinding wheel is
`R = 0.330 \ m`

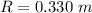
The tangential force is
`F_t = 250 \ N`

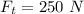
The angular acceleration is
`\alpha = 0.940 \ rad/s^2`

The torque experienced by the wheel is mathematically represented as

`\tau = I * \alpha`

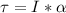
Where I is the moment of inertia

The torque experienced by the wheel can also be mathematically represented as

`\tau = F_t * r`

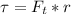
substituting values

`\tau = 250 * 0.330`

`\tau = 82.5 \ N\cdot m`

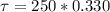
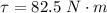
So

`82.5 = I * \alpha`

`82.5 = I * 0.940`

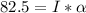
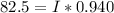
So

`I = 87.8 \ kg \cdot m^2`

This moment of inertia can be mathematically evaluated as

`I = (1)/(2) * m* r^2`

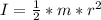
substituting values

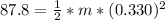
`87.8 = (1)/(2) * m* (0.330)^2`

=>
`m = 1612.5 \ kg`