Question

Are the functions f,g, and h given below linearly independent?

f(x)=e^4x
g(x)=xe^4x
h(x)=x2e^4x.

If they are independent, write all zeroes. If they are not linearly independent, find a nontrivial solution to the equation below. Be sure you can justify your answer.

A(e^4x−cos5x)+B(e^4x+cos5x)+C(cos5x)=0

Answer 1

Linearly independent, x = 0

Explanation:

- We are given three functions as follows:

`f ( x ) = e^4^x\\\\g ( x ) = xe^4^x\\\\h( x ) = x^2e^4^x`

- We are to determine the linear - independence of the given functions. We will use the theorem of linear independence which states that:

`c_1*f(x) + c_2*g(x) + c_3*h(x) = 0`

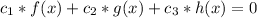
Where,

c1 , c2 , c3 are all zeroes then for all values of (x),

- The system of function is said to be linearly independent

- We will express are system of equations as such:

`c_1*e^4^x + c_2*xe^4^x + c_3*x^2e^4^x = 0\\\\`

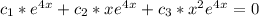
- To express our system of linear equations we will choose three arbitrary values of ( x ). We will choose, x = 0. then we have:

`c_1*( 1 ) + c_2*(0) + c_3*(0 ) = 0\\\\c_1 = 0`

- Next choose x = 1:

`c_2*e^4 + c_3*e^4 = 0\\\\c_2 + c_3 = 0`

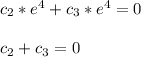
- Next choose x = 2:

`2*c_2*e^8 + 4*c_3*e^8 = 0\\\\c_2 + 2c_3 = 0`

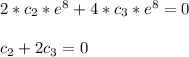
- Solve the last two equations simultaneously we have:

`c_1 = c_2 = c_3 = 0` .... ( Only trivial solution exist )

Answer: The functions are linearly independent

- The only zero exist is x = 0.