Hi,
We have the sequence 1 , 3 , 11 , 43 , __.
Let us say
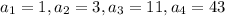 and it is required to find out
and it is required to find out
 .
.
As, we can see the pattern from the given four terms that,
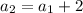 i.e.
i.e.
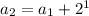
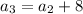 i.e.
i.e.
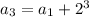
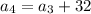 i.e.
i.e.
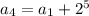
Since, the next term is obtained by adding the previous terms by odd powers of two.
Therefore,
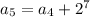 i.e.
i.e.
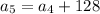 i.e
i.e
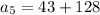 i.e.
i.e.
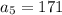
So,
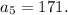
Hence, the next term of the sequence is 171.
Let us say
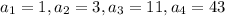 ,
,

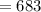 and it is required to find out
and it is required to find out
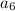 .
.
Therefore,
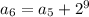 i.e.
i.e.
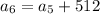 i.e
i.e
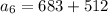 i.e.
i.e.
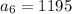
So,
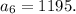
Hence, the next term of the sequence is 1195.