Answer:
1. The first function
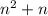 has the same order of growth as the second function
has the same order of growth as the second function
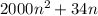 within a constant multiple.
within a constant multiple.
2. The first
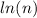 and the second
and the second
 logarithmic functions have the same order of growth within a constant multiple.
logarithmic functions have the same order of growth within a constant multiple.
3. The first function
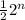 has the same order of growth as the second function
has the same order of growth as the second function
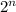 within a constant multiple.
within a constant multiple.
4. The first function
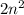 has a smaller order of growth as the second function
has a smaller order of growth as the second function
 within a constant multiple.
within a constant multiple.
Step-by-step explanation:
The given functions are
1.
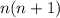 and
and
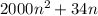
2.
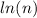 and
and

3.
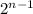 and
and
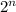
4.
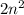 and
and

The First pair:
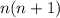 and
and
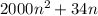
The first function can be simplified to
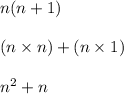
Therefore, the first function
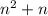 has the same order of growth as the second function
has the same order of growth as the second function
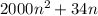 within a constant multiple.
within a constant multiple.
The Second pair:
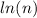 and
and

As you can notice the difference between these two functions is of logarithm base which is given by
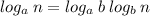
Therefore, the first
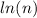 and the second
and the second
 logarithmic functions have the same order of growth within a constant multiple.
logarithmic functions have the same order of growth within a constant multiple.
The Third pair:
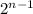 and
and
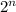
The first function can be simplified to
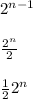
Therefore, the first function
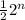 has the same order of growth as the second function
has the same order of growth as the second function
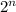 within a constant multiple.
within a constant multiple.
The Fourth pair:
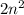 and
and

As you can notice the first function is quadratic and the second function is cubic.
Therefore, the first function
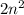 has a smaller order of growth as the second function
has a smaller order of growth as the second function
 within a constant multiple.
within a constant multiple.