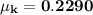Answer:
the safe's coefficient of kinetic friction on the bank floor is
Step-by-step explanation:
GIven that:
Bonnie and Clyde are sliding a 325 kg bank safe across the floor to their getaway car.
So ,let assume they are sliding the bank safe on an horizontal direction
Clyde → Δ(bank safe) → Bonnie
Also; from the above representation; let not forget that the friction force
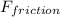 is acting in the opposite direction ←
is acting in the opposite direction ←
where;
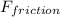 =
=
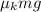
The safe slides with a constant speed
If Clyde pushes from behind with 377 N of force while Bonnie pulls forward on a rope with 353 N of force.
Thus; since the safe slides with a constant speed if the two conditions are met; then the net force acting on the slide will be equal to zero.
SO;
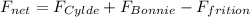
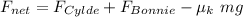
Since the net force acting on the slide will be equal to zero.
Then;
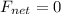
Also; let
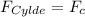 and
and
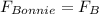
Then;
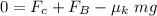
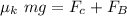
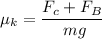
where;
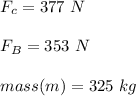
Then;
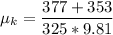

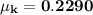
Thus; the safe's coefficient of kinetic friction on the bank floor is