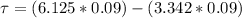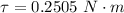Question

A string that passes over a pulley has a 0.341 kg mass attached to one end and a 0.625 kg mass attached to the other end. The pulley, which is a disk of radius 9.00 cm , has friction in its axle.What is the magnitude of the frictional torque that must be exerted by the axle if the system is to be in static equilibrium? (Answer should be in N m)

Answer 1

Answer:here to earn points

Step-by-step explanation:

Answer 2

The frictional torque is
`\tau = 0.2505 \ N \cdot m`

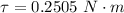
Step-by-step explanation:

From the question we are told that

The mass attached to one end the string is
`m_1 = 0.341 \ kg`

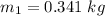
The mass attached to the other end of the string is
`m_2 = 0.625 \ kg`

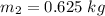
The radius of the disk is
`r = 9.00 \ cm = 0.09 \ m`

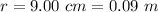
At equilibrium the tension on the string due to the first mass is mathematically represented as

`T_1 = m_1 * g`

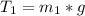
substituting values

`T_1 = 0.341 * 9.8`

`T_1 = 3.342 \ N`

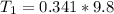
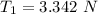
At equilibrium the tension on the string due to the mass is mathematically represented as

`T_2 = m_2 * g`

`T_2 = 0.625 * 9.8`

`T_2 = 6.125 \ N`

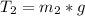
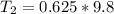
The frictional torque that must be exerted is mathematically represented as

`\tau = (T_2 * r ) - (T_1 * r )`

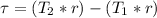
substituting values

`\tau = ( 6.125 * 0.09 ) - (3.342 * 0.09 )`

`\tau = 0.2505 \ N \cdot m`