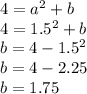Question

Find the values of a and b such that

x^2 + 3x + 4 = (x + a)^2 + b


URGENT!

*silly answers will be reported

Answer 1

a = 1.5

b = 1.75

Explanation:

First, we need to solve
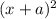`(x+a)^2` and replace the result in the initial equation as:

`x^2+3x+4=(x+a)^2+b\\x^2+3x+4=x^2+2ax+a^2+b`

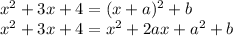
Then, this equality apply only if the coefficient of
`x` is equal in both sides and the constant is equal in both sides.

It means that we have two equations:

`3x=2ax\\4=a^2+b`

So, using the first equation and solving for a, we get:

`3x=2ax\\3=2a\\a=(3)/(2)=1.5`

Finally, replacing the value of a in the second equation and solving for b, we get:

`4=a^2+b\\4=1.5^2+b\\b=4-1.5^2\\b=4-2.25\\b=1.75`