Question

After a special medicine is introduced into a petri dish containing a bacterial culture, the number of bacteria remaining in the dish decreases rapidly. The relationship between the elapsed time ttt, in seconds, and the number of bacteria, N(t)N(t)N, left parenthesis, t, right parenthesis, in the petri dish is modeled by the following function: N(t)=4900⋅(38)t7 Complete the following sentence about the rate of change in the number of bacteria. The bacterial culture loses \dfrac{5}{8} 8 5 ​ start fraction, 5, divided by, 8, end fraction of its size every seconds.

Answer 1

7

Explanation:

khan

Answer 2

The bacterial culture loses
`(5)/(8)` of its size every 7 seconds.

Explanation:

The relationship between the elapsed time t, in seconds, and the number of bacteria, N(t), in the petri dish is modeled by the function:

`N(t)=4900\cdot\left(\frac38\right)^(t/7)`

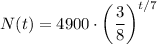
Since the growth factor is less than 1, it is a decay equation.

`\frac38=1-\frac58\\N(t)=4900\cdot\left(1-\frac58\right)^(t/7)`

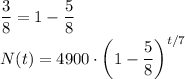
Observe that the time t is divided by 7.

This is the period.

We can therefore say that the bacterial culture loses
`(5)/(8)` of its size every 7 seconds.