2 Answers

Jeff Werner · Answer 1 · 2021-12-16T22:57:58+0000

Answer:

The correct answer is option B. AA

Explanation:

Given two triangle:

$\triangle ABC$ and
$\triangle WXY$ .

The dimensions given in
$\triangle ABC$ are:

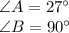
$\angle A = 27^\circ\\\angle B = 90^\circ$

We know that the sum of three angles in a triangle is equal to
$180^\circ$ .

$\angle A+\angle B+\angle C = 180^\circ\\\Rightarrow 27+90+\angle C=180^\circ\\\Rightarrow \angle C = 63^\circ$

The dimensions given in
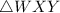$\triangle WXY$ are:

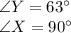
$\angle Y = 63^\circ\\\angle X = 90^\circ$

We know that the sum of three angles in a triangle is equal to
$180^\circ$ .

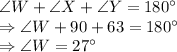
$\angle W+\angle X+\angle Y = 180^\circ\\\Rightarrow \angle W+90+63=180^\circ\\\Rightarrow \angle W = 27^\circ$

Now, if we compare the angles of the two triangles:

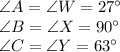
$\angle A = \angle W = 27^\circ\\\angle B = \angle X= 90^\circ\\\angle C = \angle Y= 63^\circ$

So, by AA postulate (i.e. Angle - Angle) postulate, the two triangles are similar.

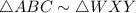$\triangle ABC \sim \triangle WXY$ by AA theorem.

So, correct answer is option B. AA

Please log in or register to add a comment.