Answer:
4,693.58 units
Step-by-step explanation:
The computation of the number of unit to be ordered is shown below:
But before that we need to find out the standard deviation of review period and the lead time which is shown below:

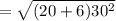
= 152.97
Now the number of units to be ordered is
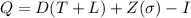
where,
T = Review period
L = Lead time
D = daily demand
I = Inventory
Z = service probability
Now placing these values to the above formula
So,
= 170 units × (20 + 6) + 2.05 × 152.97 - 40 units
= 4,420 units + 313.58 - 40 units
= 4,693.58 units
The 98% service probability is 2.05 and the same is to be considered