Answer:
Correct answer is:
The transformation was a 180° rotation about the origin.
Explanation:
Given the triangle RST formed by points:
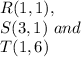
is transformed using (x, y) → (–x, –y) such that coordinates of triangle R'S'T' :
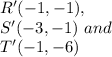
Please refer to the attached image for the given dimensions and coordinates.
It is clearly visible that:
The given triangle RST has coordinates in first quadrant.
and the resulting coordinates R'S'T' are in third quadrant.
The rotation of angle from 1st quadrant to 2nd quadrant is
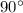 and
and
The rotation of angle from 2nd quadrant to 3rd quadrant is
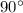 .
.
 total rotation is
total rotation is
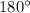 .
.