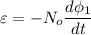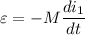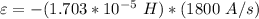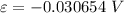Answer:
Step-by-step explanation:
From the given information:
(a)
the average magnetic flux through each turn of the inner solenoid can be calculated by the formula:
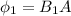
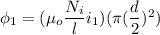
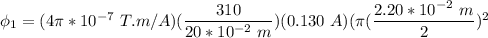

(b)
The mutual inductance of the two solenoids is calculated by the formula:
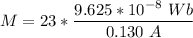
M =
 H
H
(c)
the emf induced in the outer solenoid by the changing current in the inner solenoid can be calculate by using the formula: