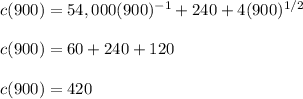Answer:
a. C(1,000) = 420,491.11
b. c(1,000) = 420.49
c. dC/dx(1,000) = 429.72
d. x = 900
e. c(900) = 420
Explanation:
We have a cost function for x units written as:
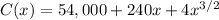
a. The total cost for x=1000 units is:
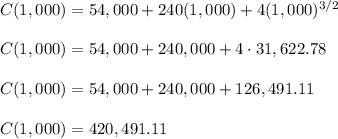
b. The average cost c(x) can be calculated dividing the total cost by the amount of units:
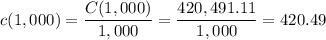
c. The marginal cost can be calculated as the first derivative of the cost function:
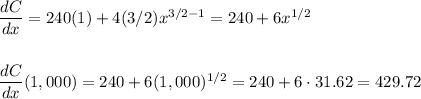
d. This value for x, that minimizes the average cost, happens when the first derivative of the average cost is equal to 0.

e. The minimum average cost is: