Question

It is estimated that 17% of the vehicles entering Canada from the United States carry undeclared goods. Use the normal approximation to calculate the probability that a search of 900 randomly selected vehicles will find more than 175 with undeclared goods.

Answer 1

The probability that a search of 900 randomly selected vehicles will find more than 175 with undeclared goods.

P( x > 175) = 0.0256

Explanation:

Step(i):-

Given sample size 'n' = 900

The estimated proportion 'p' = 0.17

Mean of the binomial distribution

μ = n p = 900 × 0.17 = 153

Standard deviation of the binomial distribution

σ =
`√(npq) = √(900 X 0.17 X 0.83) = 11.26`

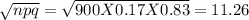
Step(ii):-

Let 'X' be the random variable of normal distribution

mean μ= 153 and σ = 11.26

Given X = 175

`Z = (175-153)/(11.268) = 1.95`

The probability that a search of 900 randomly selected vehicles will find more than 175 with undeclared goods.

P( x > 175) = P( Z> 1.95)

= 1- P( Z < 1.95)

= 1 - ( 0.5 +A( 1.95))

= 0.5 - A( 1.95)

= 0.5 - 0.4744

= 0.0256

Conclusion:-

The probability that a search of 900 randomly selected vehicles will find more than 175 with undeclared goods.

P( x > 175) = 0.0256