Question

5) Find the area of the region R that lies inside the cardioid r = 2(1+cos0) and outside the circle r = 3

Answer 1

The area is approximately 4.65263

Explanation:

Let's start by drawing the two expressions in polar coordinates to understand which area needs to be found. See the attached image for the actual area we need to find (which is highlighted in light green) that needs to be inside the cardioid and at the same time outside the circle of radius 3.

Notice that there are two points of intersection between the two curves:

One at

`r=3;\,\,and\,\,\theta=(\pi)/(3) \\and\\r=3;\,\,and\,\,\theta=-(\pi)/(3)`

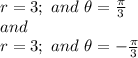
these are important points from where to calculate the appropriate integrals.

So first we calculate the area of the cardioid but limited between the values of
`-(\pi)/(3)` and
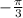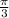`(\pi)/(3)`, and then subtract the area of the circle of radius 3 also in between the same limits for the angle
`\theta`:

`\int\limits^(\pi)/(3) _{-(\pi)/(3)} \int\limits^(2(1+cos(\theta))_0 {r\,dr} \, d\theta =\int\limits^(\pi)/(3) _{-(\pi)/(3)} (4(1+cos(\theta))^2)/(2) d\theta =2\,\int\limits^(\pi)/(3) _{-(\pi)/(3)} 1+2\,cos(\theta)+cos^2(\theta) d\theta=2\,[\theta+2\,sin(\theta)+(1)/(2) (\theta+(sin(2\theta))/(2) )]\limits^(\pi)/(3) _{-(\pi)/(3)}\approx 14.07741`

Now the integral for the circle in between those same limits for the angle
`\theta`:

`\int\limits^(\pi)/(3) _{-(\pi)/(3)} \int\limits^(3)_0 {r\,dr} \, d\theta =\ \limits^(\pi)/(3) _{-(\pi)/(3)} (3^2)/(2) \, d\theta =(9)/(2)\,(2\pi)/(3) = 3\, \pi\approx 9.42477796`

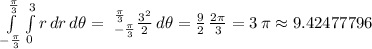
Then, the difference between both areas becomes:

14.07741 - 9.42478 = 4.65263