Assuming all points in the triangle
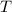 are uniformly distributed, we have the joint density
are uniformly distributed, we have the joint density
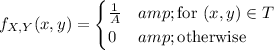
where
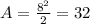 is the area of the triangle
is the area of the triangle
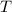 .
.
(a)
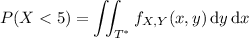
(where
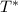 is the portion of
is the portion of
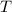 for which
for which
 is between 0 and 5)
is between 0 and 5)
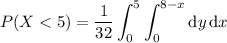
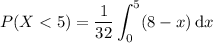
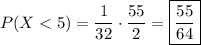
(b) Generalizing the previous result, we have
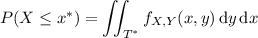
(this time with
 being the portion of
being the portion of
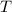 where
where
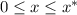 for some
for some
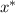 between 0 and 8)
between 0 and 8)
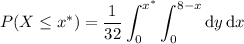
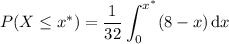
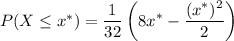
That is, the CDF of
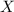 is
is
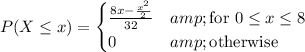
or

(c) Obtain the PDF by differentiating the CDF:
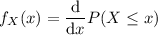
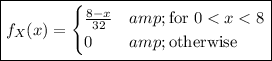
(d) Compute the expectation of
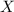 :
:
![E[X]=\displaystyle\int_0^8xf_X(x)\,\mathrm dx](https://img.qammunity.org/2021/formulas/mathematics/college/pwtzsbe81f6o7grr40rozx9ia08aei4z8n.png)
![E[X]=\displaystyle\frac1{32}\int_0^8x(8-x)\,\mathrm dx=\boxed{\frac83}](https://img.qammunity.org/2021/formulas/mathematics/college/qjlc5cuzhdxpcq657kdbgpzdrzb79j6kws.png)