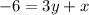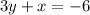Answer:
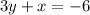
Explanation:
Given
y = 3x + 1
Required
Equation of line that passes through (12,-6) and is perpendicular to y = 3x + 1
First, the slope of the line has to be calculated;
Th slope of a line is the coefficient of x in its linear equation;
This implies that the slope of y = 3x + 1 is 3
Having calculated the slope of the first line;
The relationship between both lines are perpendicularity; this implies that
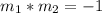
Where m_1 = 3 and m_2 is the slope of the secodnd line
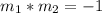 becomes
becomes
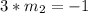
Divide both sides by 3

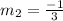
The equation of the line can be calculated using the folloing formula

Where
 and
and
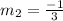
The equation becomes
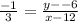
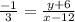
Cross multiply


Collect like terms