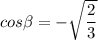Question

If the terminal ray of β lies in the third quadrant and the value of sin(β) is shown below. Determine cos(β) in the simplest form. Please show your calculations that lead to your answer.

sin(B)=-√3/3

Answer 1

`cos \beta = -\sqrt(2)/(3)`

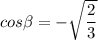
Explanation:

It is given that
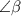`\angle \beta` lies in the third quadrant.

In 3rd quadrant, sine and cosine both are negative.

Also given that:

`sin \beta =-(\sqrt3)/(3)`

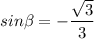
We know that identity between sine and cosine as:

`sin^2\theta + cos^2\theta = 1`

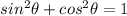
Here,
`\angle \theta\ is\ \angle \beta`

Therefore, the identity can be written as:

`sin^2\beta + cos^2\beta= 1`

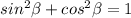
Putting the value of
`sin\beta`:

`(-(\sqrt3)/(3))^2+ cos^2\beta= 1\\\Rightarrow cos^2\beta = 1 -(3)/(9)\\\Rightarrow cos^2\beta = (9-3)/(9)\\\Rightarrow cos^2\beta = (6)/(9)\\\Rightarrow cos\beta = \pm \sqrt{(6)/(9)}\\\Rightarrow cos\beta = \pm \sqrt{(2)/(3)}`

But, it is given that
`\beta` is in 3rd quadrant. That means, value of cos
`\beta` will be negative.

Therefore, the correct answer is:

`cos \beta = -\sqrt(2)/(3)`