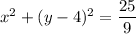Question

Which of the following is an equation of a circle in

the xy-plane with center (0, 4) and passes through (4/3,5)

Answer 1

`x^2 + (y - 4)^2 = (25)/(9)`

Explanation:

The equation of a circle with center at (h, k) and radius r is

`(x - h)^2 + (y - k)^2 = r^2`

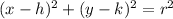
You have center (0, 4).

We get:

`(x - 0)^2 + (y - 4)^2 = r^2`

`x^2 + (y - 4)^2 = r^2`

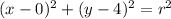
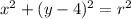
To find the radius, we use the distance formula to find the distance from the center of the circle to the given point on the circle.

`r = d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

`r = \sqrt{((4)/(3) - 0)^2 + (5 - 4)^2}`

`r = \sqrt{((4)/(3))^2 + 1^2}`

`r = \sqrt{(16)/(9) + (9)/(9)}`

`r = \sqrt{(25)/(9)}`

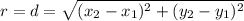
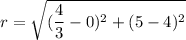
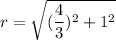
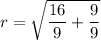
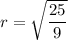
We need r^2 in the equation of the circle, so

`r^2 = (25)/(9)`

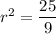
The equation of the circle is

`x^2 + (y - 4)^2 = (25)/(9)`