Question

Show work and Factor 4x^2+xy-18y^2

Answer 1

`4x^2+xy-18y^2=(4x+9y)\,(x-2y)`

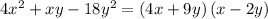
Explanation:

Let's examine the following general product of two binomials with variables x and y in different terms:

`(ax+by)\,(cx+dy)= ac\,x^2+adxy+bcxy+bdy^2`

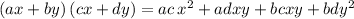
so we want the following to happen:

`a\,c = 4\\ad+bc=1\\bd--18`

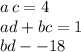
Notice as well that
`ad+bc =1` means that those two products must differ in just one unit so, one of them has to be negative, or three of them negative. Given that the product
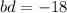`bd=-18`, then we can consider the case in which one of this (b or d) is the negative factor. So let's then assume that
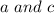`a\,\,and \,\,c` are positive.

We can then try combinations for
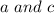`a\,\,and \,\,c` such as:

`a = 4;\,\,c=1\\a=2;\,\,c=2\\a=1;\,\,c=4`

Just by selecting the first one
`(a=4;\,\,c=1)`

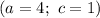
we get that
`4d_b=1\\b=-4d-1`

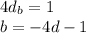
and since

`bd=-18\\(-4d-1)\,d=-18\\-4d^2-d=-18\\4d^2+d-18=0`

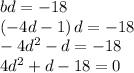
This quadratic equation give as one of its solutions the integer: d = -2, and consequently,

`d=-18/(-2)\\d=9`

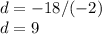
Now we have a good combination of parameters to render the factoring form of the original trinomial:

`a=4; \,\,b=9;\,\,c=1;\,\,d=-2`

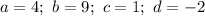
which makes our factorization:

`(4x+9y)\,(x-2y)=4x^2+xy-18y^2`