Answer:
(a) The rate of change for the money earned, measured as dollars per delivery, between 0 and 2 deliveries is $2.
(b) The rate of change is the same between the two time intervals.
Explanation:
The rate of change for a variables based on another variable is known as the slope.
The formula to compute the slope is:

(a)
Compute the rate of change for the money earned, measured as dollars per delivery, between 0 and 2 deliveries as follows:
For, x₁ = 0 and x₂ = 2 deliveries the money earned are y₁ = $5 and y₂ = $9.
The rate of change for the money earned is:

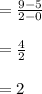
Thus, the rate of change for the money earned, measured as dollars per delivery, between 0 and 2 deliveries is $2.
(b)
Compute the rate of change for the money earned, measured as dollars per delivery, between 2 and 4 deliveries as follows:
For, x₁ = 2 and x₂ = 4 deliveries the money earned are y₁ = $9 and y₂ = $13.
The rate of change for the money earned is:

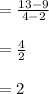
The rate of change for the money earned, measured as dollars per delivery, between 2 and 4 deliveries is $2.
Compute the rate of change for the money earned, measured as dollars per delivery, between 6 and 8 deliveries as follows:
For, x₁ = 6 and x₂ = 8 deliveries the money earned are y₁ = $17 and y₂ = $21.
The rate of change for the money earned is:

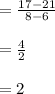
The rate of change for the money earned, measured as dollars per delivery, between 6 and 8 deliveries is $2.
Thus, the rate of change is the same between the two time intervals.