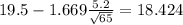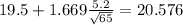Question

Sales personnel for Skillings Distributors submit weekly reports listing the customer contacts made during the week. A sample of 6565 weekly reports showed a sample mean of 19.519.5 customer contacts per week. The sample standard deviation was 5.2.5.2. Provide 90%90% and 95%95% confidence intervals for the population mean number of weekly customer contacts for the sales personnel.

Answer 1

95% confidence

`19.5-1.998(5.2)/(√(65))=18.211`

`19.5+1.998(5.2)/(√(65))=20.789`

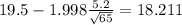
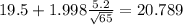
For the 90% confidence interval the critical value would be
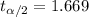`t_(\alpha/2)=1.669` and replacing we got:

`19.5-1.669(5.2)/(√(65))=18.424`

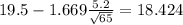
`19.5+1.669(5.2)/(√(65))=20.576[/tex</p><p><strong>Step-by-step explanation:</strong></p><p><strong>Information given</strong></p><p>[tex]\bar X=19.5` represent the sample mean

`\mu` population mean (variable of interest)

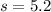`s=5.2` represent the sample standard deviation

n=65 represent the sample size

Confidence interval

The confidence interval for the mean is given by the following formula:

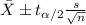`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The degrees of freedom are given by:

`df=n-1=65-1=64`

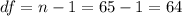
Since the Confidence is 0.95 or 95%, the value of
`\alpha=0.05` and
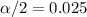`\alpha/2 =0.025`, and the critical value would be
`t_(\alpha/2)=1.998`

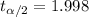
Now we have everything in order to replace into formula (1):

`19.5-1.998(5.2)/(√(65))=18.211`

`19.5+1.998(5.2)/(√(65))=20.789`

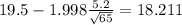
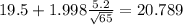
For the 90% confidence interval the critical value would be
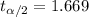`t_(\alpha/2)=1.669` and replacing we got:

`19.5-1.669(5.2)/(√(65))=18.424`

`19.5+1.669(5.2)/(√(65))=20.576`