Question

A puck on the ice travels 20.0 m [25° W of N], gets deflected, and travels 30.0 m [35° N of W]. Determine where the puck will end up with respect to its starting point, which is the puck's total displacement, using the tail-to-tip with math (trigonometry) method. In the same hockey game, a player is positioned 35 m [40° W of S] of the net. He shoots the puck 25 m [E] to a teammate. What second displacement does the teammate shoot the puck with in order to make it to the net? Find the answer using the component method.

Answer 1

Given that,

Ice travel = 20.0 m

The direction is 25° W of N

Deflect distance = 30.0 m

The direction is 35° N of W

(I). When ice travel west of north

We need to calculate the displacement

Using formula of displacement of component

`\vec{D}=d\cos\theta+d\sin\theta`

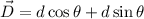
Put the value into the formula

`\vec{D}=20\cos25(j)+20\sin25(-i)`

`\vec{D}=18j-8.44i`

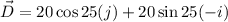
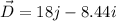
(II). When ice deflect north of west

We need to calculate the displacement

Using formula of displacement of component

`\vec{D'}=d\cos\theta+d\sin\theta`

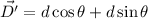
Put the value into the formula

`\vec{D'}=30\cos35(-i)+30\sin35(j)`

`\vec{D'}=-24.3i+17.1j`

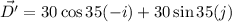
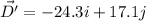
We need to calculate the magnitude puck's total displacement

Using formula for total displacement

`\vec{D''}=\vec{D}+\vec{D'}`

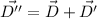
Put the value into the formula

`\vec{D''}=18j-8.44i-24.3i+17.1j`

`\vec{D''}=-32.74i+35.1j`

`|\vec{D''}|=√((-32.74)^2+(35.1)^2)`

`D''=47.9\ m`

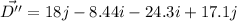
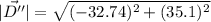
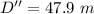
Hence, The magnitude puck's total displacement is 47.9 m.

(ii). Given that,

He shoot the puck 25 m in east.

The displacement is

`\vec{D}=25i+0j`

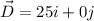
A player is positioned 35 m at 40° West of south.

We need to calculate the displacement

Using formula of displacement

`\vec{D'}=d\cos\theta(-i)+d\sin\theta(-j)`

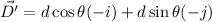
Put the value into the formula

`\vec{D'}=35\cos40(-i)+35\sin40(-j)`

`\vec{D'}=-26.81i-22.49j`

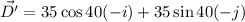
We need to calculate the total displacement

Using formula for total displacement

`\vec{D''}=\vec{D}+\vec{D''}`

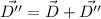
Put the value into the formula

`\vec{D''}=25i+0j-26.81i-22.49j`

`\vec{D''}=-1.81i-22.49j`

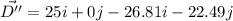
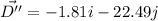
The magnitude of the total displacement

`|\vec{D''}|=√((-1.81)^2+(-22.49)^2)`

`D''=22.56\ m`

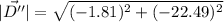
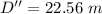
Hence, The magnitude of the total displacement is 22.56 m