Question

In the game of​ roulette, a player can place a ​$10 bet on the number 19 and have a StartFraction 1 Over 38 EndFraction

probability of winning. If the metal ball lands on 19​, the player gets to keep the ​$10 paid to play the game and the player is awarded an additional ​$350. ​Otherwise, the player is awarded nothing and the casino takes the​ player's ​$10. What is the expected value of the game to the​ player? If you played the game 1000​ times, how much would you expect to​ lose? Note that the expected value is the​ amount, on​ average, one would expect to gain or lose each game.

Answer 1

(a)-$0.53

(b)$530

Explanation:

If the player wins the game, he gets a profit of $350.

If the player losses the game, he gets a profit of -$10.

Probability of Winning
`=(1)/(38)`

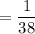
Probability of Loosing
`=(37)/(38)`

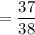
(a)Expected Value of the game

`E(x)=\left((1)/(38) * 350\right) + \left((37)/(38) * -10\right)\\=-\$0.53`

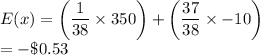
The expected value of the game to the player is -$0.53.

(b)If the game is played 1000 times

Expected Loss = 0.53 X 1000

=$530

The player should expect to lose approximately $530 if he plays the game 1000 times.