Answer:
B = 0.024T positive z-direction
Step-by-step explanation:
In this case you consider that the direction of the motion of the electron, and the direction of the magnetic field are perpendicular.
The magnitude of the magnetic force exerted on the electron is given by the following formula:
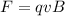 (1)
(1)
q: charge of the electron = 1.6*10^-19 C
v: speed of the electron = 1.6*10^7 m/s
B: magnitude of the magnetic field = ?
By the Newton second law you also have that the magnetic force is equal to:
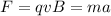 (2)
(2)
m: mass of the electron = 9.1*10^-31 kg
a: acceleration of the electron = 7.0*10^16 m/s^2
You solve for B from the equation (2):

The direction of the magnetic field is found by using the right hand rule.
The electron moves upward (+^j). To obtain a magnetic forces points to the positive x-direction (+^i), the direction of the magnetic field has to be to the positive z-direction (^k). In fact, you have:
-^j X ^i = ^k
Where the minus sign of the ^j is because of the negative charge of the electron.
Then, the magnitude of the magnetic field is 0.024T and its direction is in the positive z-direction