Question

A human resource manager for a large company takes a random sample of 60 employees from the company database. Based on the sample she calculates a 95% confidence interval for the mean time of employment for all employees to be 8.7 to 15.2 years. Which of the following will provide a more informative (i.e., narrower) confidence interval than the 95% confidence interval?

A. Using a 90% confidence level (instead of 95%)
B. Using a 99% confidence level (instead of 95%)
C. Using a sample size of 40 employees (instead of 60)
D. Using a sample size of 90 employees (instead of 60)

Answer 1

A. Using a 90% confidence level (instead of 95%)

D. Using a sample size of 90 employees (instead of 60)

Explanation:

The margin of error of a confidence interval is given by:

`M = z*(\sigma)/(√(n))`

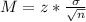
In which z is related to the confidence level,
`\sigma` is the standard deviation of the population and n is the size of the sample.

The higher the margin of error, the less precise the confidence interval is.

We have:

A 95% confidence interval, with a sample of 60.

We want to make it more precise:

Two options, decrease z(decrease the confidence level), or increase n(increase the sample size).

So the correct options are:

A. Using a 90% confidence level (instead of 95%)

D. Using a sample size of 90 employees (instead of 60)