Answer:
A. Using a 90% confidence level (instead of 95%)
D. Using a sample size of 90 employees (instead of 60)
Explanation:
The margin of error of a confidence interval is given by:
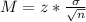
In which z is related to the confidence level,
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
The higher the margin of error, the less precise the confidence interval is.
We have:
A 95% confidence interval, with a sample of 60.
We want to make it more precise:
Two options, decrease z(decrease the confidence level), or increase n(increase the sample size).
So the correct options are:
A. Using a 90% confidence level (instead of 95%)
D. Using a sample size of 90 employees (instead of 60)