Question

A set of shirt prices are normally distributed with a mean of 45 dollars and a standard deviation of 5 dollars. What proportion of shirt prices are between 37 dollars and 59.35 dollars? You may round your answer to four decimal places.

Answer 1

0.9432

Explanation:

Given that

`\\Mean (\mu)= 45`

`Standard\;Deviation (\sigma)= 5`

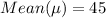
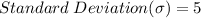
Based on this, the proportion of the shirt price between the given range is

As we know that

For 37 dollars

`z_( score ) = (x-\mu)/(\sigma)`

`z = (37.0-45.0)/(5.0)`

`z_1 = -1.6`

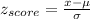
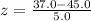
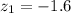
For 59.35 dollars

`\\ z = (59.35-45.0)/(5.0) \\`

`z_2 = 2.87`

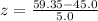
This results into

= P(37.0 < x < 59.35)

= P(-1.6 < z < 2.87)

= P(Z < 2.87) - P(Z < -1.6)

So,

= P(37.0 < x < 59.35)

= 0.9979 - 0.0547

= 0.9432

Refer to Z score table