Question

Use the Central Limit Theorem to find a mean given a probability Question A video game company sells an average of 132 games a month, with a standard deviation of 9 games. The company is looking to reward stores that are selling in the top 7%. How many video games must a store sell in order to be eligible for a reward if the company is only looking at 36 of their stores. Use the 2-table below: z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 1.1 0.864 0.867 0.869 0.871 0.873 0.875 0.877 0.879 0.881 0.883 1.2 0.885 0.887 0.889 0.891 0.893 0.894 0.896 0.898 0.900 0.901 1.3 0.9030.905 0.9070.908 0.910 0.911 0.913 0.915 0.9160.918 1.4 0.919 0.921 0.922 0.924 0.925 0.926 0.928 0.929 0.931 0.932 1.5 0.933 0.934 0.936 0.937 0.938 0.939 0.941 0.942 0.943 0.944 1.6 0.945 0.946 0.947 0.948 0.949 0.951 0.952 0.953 0.954 0.954

Round the z.score and a to two decimal places. Round up to the nearest whole number.

Answer 1

1.48

1.5

135

Explanation:

Answer 2

The number of games must a store sell in order to be eligible for a reward is 135.

Explanation:

Let the random variable X represent the number of video games sold in a month by the sores.

The random variable X has a mean of, μ = 132 and a standard deviation of, σ = 9.

It is provided that the company is looking to reward stores that are selling in the top 7%.

That is,
`P (\bar X > \bar x) = 0.07`.

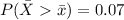The z-score related to this probability is, z = 1.48.

Compute the number of games must a store sell in order to be eligible for a reward as follows:

`z=(\bar x-\mu)/(\sigma/√(n))`

`\bar x=\mu+z\cdot \sigma/√(n)`

`=132+1.48* (9/√(36))\\\\=132+2.22\\\\=134.22\\\\\approx 135`

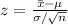
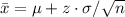
Thus, the number of games must a store sell in order to be eligible for a reward is 135.