Question

The average American generates 4.4 lbs of trash every day. We circulated fliers that listed tips on how to reduce wastefulness in three separate neighborhoods. For the next week, we measured the amount of trash each person produced each day in those neighborhoods. There were 625 people total in our study. The mean trash per person was 4.3 lbs with a standard deviation of 1

Determine your sample's score on the comparison distribution.
a) -2
b) -1
c) -1.5
d) -2.5

Answer 1

`z= (\bar X -\mu)/((\sigma)/(√(n)))`

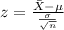
And replacing we got:

`z=(4.3 -4.4)/((1)/(√(625)))= -2.5`

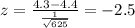
And the best option would be:

d) -2.5

Explanation:

For this problem we know that the true mean of trash every day is:

`\mu =4.4`

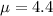
And from the info given we also know that:

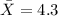`\bar X=4.3` represent the sample mean

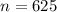`n=625` sample size selected

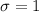`\sigma = 1` the population standard deviation assumed

If we want to find the z score for the person we can use the following formula:

`z= (\bar X -\mu)/((\sigma)/(√(n)))`

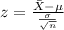
And replacing we got:

`z=(4.3 -4.4)/((1)/(√(625)))= -2.5`

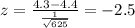
And the best option would be:

d) -2.5