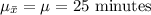Answer:
(a)
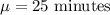
(b)
(c)
 .
.
(d)
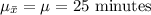
Explanation:
Let the random variable X represent the time it takes a certain brand of ibuprofen to start working.
(a)
The mean time it takes a certain brand of ibuprofen to start working is, 25 minutes.
That is,
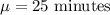 .
.
(b)
The standard deviation of time it takes a certain brand of ibuprofen to start working is, 13 minutes.
That is,
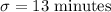 .
.
(c)
The sample selected by a pharmacist is of size, 20.
That is,
 .
.
(d)
The mean of the sample means is: