Answer:
Explanation:
To find the extremum of the function, you need to take the first derivative.
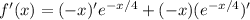

This derivative = 0 if and only if x - 4 = 0, hence the extremum is at x = 4
To consider if it is local max or min, you need to consider the act of the function before and after x = 4 by making a table.
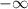 4
4
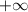
f(x) - 0 +
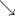
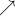
Hence x =4 is a local min.