Question

A researcher would like to estimate p, the proportion of U.S. adults who support recognizing civil unions between gay or lesbian couples.

Due to a limited budget, the researcher obtained opinions from a random sample of only 2,222 U.S. adults. With this sample size, the researcher can be 95% confident that the obtained sample proportion will differ from the true proportion (p) by no more than (answers are rounded):
(a) .04%
(b) .75%
(c) 2.1%
(d) 3%
(e) There is no way to figure this out without knowing the actual sample proportion that was obtained

Answer 1

`$ SE = 1.96\cdot \sqrt{(0.50(1-0.50))/(2222) } $`

`SE = 1.96\cdot 0.0106 \\\\SE = 0.021\\\\SE = 2.1 \: \%`

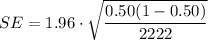
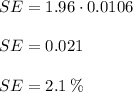
The correct option is

(c) 2.1%

Therefore, with a sample size of 2,222, the researcher can be 95% confident that the obtained sample proportion will differ from the true proportion (p) by no more than 2.1%

Explanation:

The obtained sample proportion will differ from the true proportion (p) by

`$ SE = z\cdot \sqrt{(p(1-p))/(n) } $`

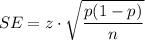
It is known as standard error or margin of error.

Where p is the sample proportion and n is the sample size.

Since we are not given p then we would assume

p = 0.50

That would maximize the error just to be on the safe side.

The z-score corresponding to 95% confidence level is given by

Level of significance = 1 - 0.95 = 0.05/2 = 0.025

From the z-table, the z-score corresponding to probability of 0.025 is

z-score = 1.96

So the error is

`$ SE = 1.96\cdot \sqrt{(0.50(1-0.50))/(2222) } $`

`SE = 1.96\cdot 0.0106 \\\\SE = 0.021\\\\SE = 2.1 \: \%`

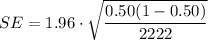
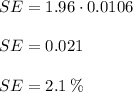
So the correct option is

(c) 2.1%

Therefore, with a sample size of 2,222, the researcher can be 95% confident that the obtained sample proportion will differ from the true proportion (p) by no more than 2.1%