Answer:
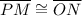 :, Segment subtended by the same angle on two adjacent parallel lines are congruent
:, Segment subtended by the same angle on two adjacent parallel lines are congruent
Explanation:
Statement, Reason
MNOP is a parallelogram:, Given
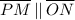 :, Opposite sides of a parallelogram
:, Opposite sides of a parallelogram
∠PMO ≅ ∠MON:, Alternate Int. ∠s Thm.
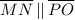 :, Opposite sides of a parallelogram
:, Opposite sides of a parallelogram
∠POM ≅ ∠NMO:, Alternate Int. ∠s Thm.
OM ≅ OM:, Reflexive property
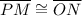 :, Segment subtended by the same angle and on two adjacent parallel lines are congruent
:, Segment subtended by the same angle and on two adjacent parallel lines are congruent