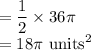Answer:
The ratio of the measure of the central angle to the entire circle measure
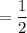
The area of the entire circle

The area of the sector
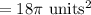
Explanation:
MNL is a diameter of the circle N
Radius, NL =6
- The measure of central angle MNL = π radians
- The measure of the entire circle = 2π radians.
The ratio of the measure of the central angle to the entire circle measure

Area of a circle
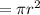
The area of the entire circle
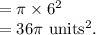
Therefore, the area of the sector