Question

You are trying to overhear a juicy conversation, but from your distance of 25.0 m, it sounds like only an average whisper of 25.0 dB. So you decide to move closer to give the conversation a sound level of 80.0 dB instead. How close should you come?

Answer 1

r₂ = 1,586 m

Step-by-step explanation:

For this problem we are going to solve it by parts, let's start by finding the sound intensity when we are 25 m

β = 10 log (I / I₀)

where Io is the sensitivity threshold 10⁻¹² W / m²

I₁ / I₀ =
`e^(\beta/10)`

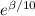
I₁ = I₀ e^{\beta/10}

let's calculate

I₁ = 10⁻¹² e^{25/10}

I₁ = 1.20 10⁻¹¹ W / m²

the other intensity in exercise is

I₂ = 10⁻¹² e^{80/10}

I₂ = 2.98 10⁻⁹ W / m²

now we use the definition of sound intensity

I = P / A

where P is the emitted power that is a constant and A the area of ​​the sphere where the sound is distributed

P = I A

the area a sphere is

A = 4π r²

we can write this equation for two points of the found intensities

I₁ A₁ = I₂ A₂

where index 1 corresponds to 25m and index 2 to the other distance

I₁ 4π r₁² = I₂ 4π r₂²

I₁ r₁² = I₂ r₂²

r₂ = √ (I₁ / I₂) r₁

let's calculate

r₂ = √ (1.20 10⁻¹¹ / 2.98 10⁻⁹) 25

r₂ = √ (0.40268 10⁻²) 25

r₂ = 1,586 m