Question

If you're good at quadratic equations please help meee

For what two values of k does x^2+kx+9=0 have only one solution?

Answer 1

k = 6 OR k = -6

Explanation:

Given Equation is:

=>
`x^2+kx+9=0`

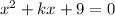
To Find the value of k, we'll find it's discriminant:

Comparing the above equation with standard form of quadratic equation, we get:

a = 1, b = k and c = 9

=> Discriminant =
`b^2-4ac`

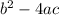
D =
`(k)^2-4(1)(9)`

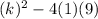
D =
`k^2-36`

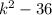
Given that Equation has only one solution, So D will be equal to 0

0 =
`k^2-36`

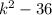
Adding 36 to both sides

`k^2 = 36`

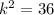
Taking sqrt on both sides

=> k = ±6

Either,

k = 6 OR k = -6

Answer 2

x² + kx + 9 = 0

To find the possible values of k first calculate the discriminant D

D = b² - 4ac

where

a = 1 b = k and c = 9

D = k ² - 4(1)(9)

D = k² - 36

For the above equation to have one solution D must be equal to zero

That's

D = 0

We get

k² - 36 = 0

(k+6)(k -6) = 0

k = 6 k = - 6

Therefore the two values of k which make

x² + kx + 9 have only one solution is

6 and - 6

Hope this helps.