Question

Assume that a sample is used to estimate a population proportion p. Find the 98% confidence interval for a

sample of size 131 with 81% successes. Enter your answer as a tri-linear inequality using decimals (not
percents) accurate to three decimal places.
apa
> Next Question

Answer 1

`0.81 - 2.326 \sqrt{(0.81(1-0.81))/(131)}=0.730`

`0.81 + 2.326 \sqrt{(0.81(1-0.81))/(131)}=0.890`

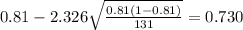
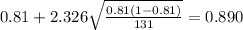
And the confidence interval would be:

`0.730 \leq \p \leq 0.890`

Explanation:

Information given:

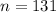`n=131` represent the sample size

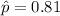`\hat p=0.81` represent the estimated proportion

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

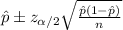
For the 98% confidence interval the value of
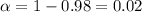`\alpha=1-0.98=0.02` and
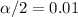`\alpha/2=0.01`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=2.326`

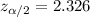
And replacing into the confidence interval formula we got:

`0.81 - 2.326 \sqrt{(0.81(1-0.81))/(131)}=0.730`

`0.81 + 2.326 \sqrt{(0.81(1-0.81))/(131)}=0.890`

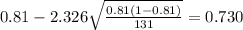
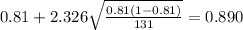
And the confidence interval would be:

`0.730 \leq \p \leq 0.890`