The polynomial x^2+3x-1 is a factor of x^4+3x^3-2x^2-3x+1 true or false?

Question

asked May 3, 2021 63.6k views

1 Answer

Steven Carlson · Answer 1 · 2021-05-08T18:01:57+0000

Answer:

Yes, it is true that
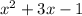x^2+3x-1 is a factor of
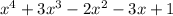x^4+3x^3-2x^2-3x+1 .

Explanation:

Let us try to factorize
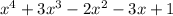
x^4+3x^3-2x^2-3x+1

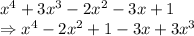
$x^4+3x^3-2x^2-3x+1\\\Rightarrow x^4-2x^2+1-3x+3x^3$

Let us try to make a whole square of the given terms:

$\Rightarrow (x^2)^2-2* x^2 * 1+1^2+3x^3-3x\\\Rightarrow (x^2-1)^2+3x^3-3x\\$

--------------

Formula used above:

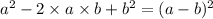
a^(2) -2 * a * b +b^(2) = (a-b)^2

In the above equation, we had
a = x, b = 1 .

--------------

Further solving the above equation, taking
common out of
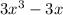
3x^3-3x

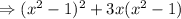
$\Rightarrow (x^2-1)^2+3x(x^2-1)\\$

Taking
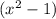(x^(2) -1) common out of the above term:

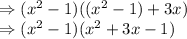
$\Rightarrow (x^2-1)((x^2-1)+3x)\\\Rightarrow (x^2-1)(x^2+3x-1)$

So, the two factors are
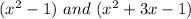$(x^2-1)\ and\ (x^2+3x-1)$ .

$\therefore$ The statement that
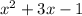x^2+3x-1 is a factor of
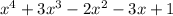x^4+3x^3-2x^2-3x+1 is True.