Question

Abinomial probability experiment is conducted with the given parameters. Compute the probability of x successes in the n independent trials of the experime

n=10, p=0.4.X=4
P(4)=
(Do not round unul the final answer. Then round to four decimal places as needed.)​

Answer 1

The probability of exactly '4' success

P( X=4) = 0.2508

Explanation:

Step(i):-

Given sample size 'n' = 10

Given probability of success 'p' = 0.4

q = 1 -p = 1 - 0.4 = 0.6

Step(ii):-

Let 'X' be the successes in binomial distribution

`P( x = r) = n_{C_(r) } p^(r) q^(n-r)`

The probability of exactly '4' success

`P( x = 4) = 10_{C_(4) } (0.4)^(4) (0.6)^(10-4)`

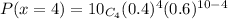
we will use factorial notation

`10C_(4) = (10!)/((10-4)!4!) = (10 X 9 X 8 X 7 X6!)/(6! 4!) = (10 X 9 X8 X7)/(4X 3X 2X1) = 210`

`P( x = 4) = 210 X 0.0256 X0.0466`

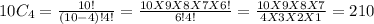
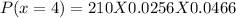
P( X=4) = 0.2508

conclusion:-

The probability of exactly '4' success

P( X=4) = 0.2508