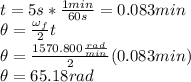Question

1. Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.00 s. Radius of tire is 50 cm. What angle did the tire move through in those 5 secs

Answer 1

`\theta=65.18rad`

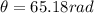
Step-by-step explanation:

The angle in rotational motion is given by:

`\theta=(w_o+w_f)/(2)t`

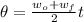
Recall that the angular speed is larger than regular frequency (in rpm) by a factor of
`2\pi`, so:

`\omega_f=2\pi f\\\omega_f=2\pi*250rpm\\\omega_f=1570.80 (rad)/(min)`

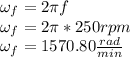
The wheel spins from rest, that means that its initial angular speed is zero(
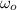`\omega_o`). Finally, we have to convert the given time to minutes and replace in the first equation:

`t=5s*(1min)/(60s)=0.083min\\\theta=(\omega_f)/(2)t\\\theta=(1570.800(rad)/(min))/(2)(0.083min)\\\theta=65.18rad`