Answer:
1) The probability that a person who tests positive actually has the disease is 0.1056 or 10.56%
2) 180 combinations
3) 5040 pin numbers can be chosen
4) 54439560 ways
5) 389283935040 ways
Explanation:
1) From Bayes' theorem, we have;
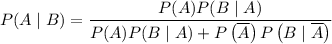
Where:
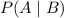 = Percentage of the population that tests positive for the disease that actually have the disease
= Percentage of the population that tests positive for the disease that actually have the disease
P(A) = Incidence rate = 0.5% = 0.005
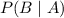 = Percentage of the population that have the disease and will tests positive = 1 - 0.06 = 0.94
= Percentage of the population that have the disease and will tests positive = 1 - 0.06 = 0.94
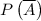 = P(no disease) = 1 - 0.005 = 0.995
= P(no disease) = 1 - 0.005 = 0.995
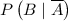 = P(positive
= P(positive
 no disease) = False positive = 0.04
no disease) = False positive = 0.04
From which we have;

Therefore, the probability that a person who tests positive actually has the disease = 0.1056 or 10.56%
2) The parameters given are;
The number of shirts that Karla has = 10 shirts
The number of shorts that Karla has = 6 shorts
The number of pairs of sandals that Karla has = 3 pairs
Therefore;
The number of ways Karla can choose her shirts = 10 ways
The number of ways Karla can choose her shorts = 6 ways
The number of ways Karla can choose her pair of sandals = 3 ways
The total combination of outfits Karla can make = 10 × 6 × 3 = 180 combinations
3) We have;
The number of permutations of 10 numbers taking 4 at a time is given as follows;
n!/(n-r)! = 10!/(10-4)! = 10!/6! = 5040 pin numbers can be chosen
4) The number of ways the first second and the third can be awarded is 380×379×378 = 54439560 ways
5) The number of ways is 210×209×208×207×206 = 389283935040 ways.