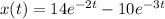Answer:
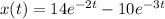
Explanation: In a mass-spring-damper system, the differential equation that rules the motion of the mass is: mx" + cx' + kx = 0
Using m = 4, k = 24 and c = 20, we have
4x" + 20x' + 24x = 0
Simplifying, we have
x" + 5x'+ 6x = 0
The characteristic equation of this differential is
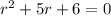
The solutions for the quadratic equation are:
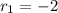 and
and
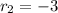
Hence:
x(t) =
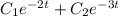
x'(t) =
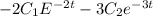
To determine the constants, we have the initial conditions x(0) = 4 and
x'(0) = 2, then:


Substituing the constants:
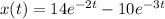
The position function for this system is: