Question

Suppose the proportion X of surface area in a randomly selected quadrat that is covered by a certain plant has a standard beta distribution with α = 4 and β = 3.(a) Compute E(X) and V(X). (Round your answers to four decimal places.)E(X) = Correct: Your answer is correct.V(X) = Correct: Your answer is correct.(b) Compute P(X ≤ 0.5). (Round your answer to four decimal places.)

Answer 1

(a) The value of E (X) is 4/7.

The value of V (X) is 3/98.

(b) The value of P (X ≤ 0.5) is 0.3438.

Explanation:

The random variable X is defined as the proportion of surface area in a randomly selected quadrant that is covered by a certain plant.

The random variable X follows a standard beta distribution with parameters α = 4 and β = 3.

The probability density function of X is as follows:

`f(x) = (x^(\alpha-1)(1-x)^(\beta-1))/(B(\alpha,\beta)) ; \hspace{.3in}0 \le x \le 1;\ \alpha, \beta > 0`

Here, B (α, β) is:

`B(\alpha,\beta)=((\alpha-1)!\cdot\ (\beta-1)!)/(((\alpha+\beta)-1)!)`

`=((4-1)!\cdot\ (3-1)!)/(((4+3)-1)!)\\\\=(6* 2)/(720)\\\\=(1)/(60)`

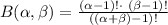
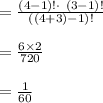
So, the pdf of X is:

`f(x) = (x^(4-1)(1-x)^(3-1))/(1/60)=60\cdot\ [x^(3)(1-x)^(2)];\ 0\leq x\leq 1`

(a)

Compute the value of E (X) as follows:

`E (X)=(\alpha )/(\alpha +\beta )`

`=(4)/(4+3)\\\\=(4)/(7)`

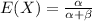
The value of E (X) is 4/7.

Compute the value of V (X) as follows:

`V (X)=(\alpha\ \cdot\ \beta)/((\alpha+\beta)^(2)\ \cdot\ (\alpha+\beta+1))`

`=(4\cdot\ 3)/((4+3)^(2)\cdot\ (4+3+1))\\\\=(12)/(49* 8)\\\\=(3)/(98)`

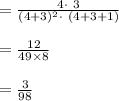
The value of V (X) is 3/98.

(b)

Compute the value of P (X ≤ 0.5) as follows:

`P(X\leq 0.50) = \int\limits^(0.50)_(0){60\cdot\ [x^(3)(1-x)^(2)]} \, dx`

`=60\int\limits^(0.50)_(0){[x^(3)(1+x^(2)-2x)]} \, dx \\\\=60\int\limits^(0.50)_(0){[x^(3)+x^(5)-2x^(4)]} \, dx \\\\=60* [(x^4)/(4)+(x^6)/(6)-(2x^5)/(5)]\limits^(0.50)_(0)\\\\=60* [(x^4\left(10x^2-24x+15\right))/(60)]\limits^(0.50)_(0)\\\\=[x^4\left(10x^2-24x+15\right)]\limits^(0.50)_(0)\\\\=0.34375\\\\\approx 0.3438`

Thus, the value of P (X ≤ 0.5) is 0.3438.