Question

A cart of mass 350 g is placed on a frictionless horizontal air track. A spring having a spring constant of 7.5 N/m is attached between the cart and the left end of the track. The cart is displaced 3.8 cm from its equilibrium position. (a) Find the period at which it oscillates. s (b) Find its maximum speed. m/s (c) Find its speed when it is located 2.0 cm from its equilibrium position.

Answer 1

(a) T = 1.35 s

(b) vmax = 0.17 m/s

(c) v = 0.056 m/s

Step-by-step explanation:

(a) In order to calculate the period of oscillation you use the following formula for the period in a simple harmonic motion:

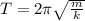`T=2\pi\sqrt{(m)/(k)}` (1)

m: mass of the cart = 350 g = 0.350kg

k: spring constant = 7.5 N/m

`T=2\pi \sqrt{(0.350kg)/(7.5N/m)}=1.35s`

The period of oscillation of the car is 1.35s

(b) The maximum speed of the car is given by the following formula:

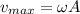`v_(max)=\omega A` (2)

w: angular frequency

A: amplitude of the motion = 3.8 cm = 0.038m

You calculate the angular frequency:

`\omega=(2\pi)/(T)=(2\pi)/(1.35s)=4.65(rad)/(s)`

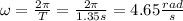
Then, you use the result of w in the equation (2):

`v_(max)=(4.65rad/s)(0.038m)=0.17(m)/(s)`

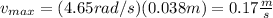
The maximum speed if 0.17m/s

(c) To find the speed when the car is at x=2.0cm you first calculate the time t by using the following formula:

`x=Acos(\omega t)\\\\t=(1)/(\omega)cos^(-1)((x)/(A))\\\\t=(1)/(4.65rad/s)cos^(-1)((0.02)/(0.038))=0.069s`

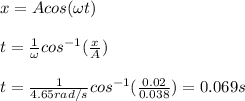
The speed is the value of the following function for t = 0.069s

`|v|=|\omega A sin(\omega t)|\\\\|v|=(4.65rad/s)(0.038m)sin(4.65rad/s (0.069s))=0.056(m)/(s)`

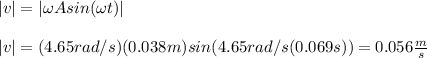
The speed of the car is 0.056m/s