Question

Would apreciate if someone helped me..

Answer 1

a). x = 11

b). m∠DMC = 39°

c). m∠MAD = 66°

d). m∠ADM = 36°

e). m∠ADC = 18°

Explanation:

a). In the figure attached,

m∠AMC = 3x + 6

and m∠DMC = 6x - 49

Since "in-center" of a triangle is a points where the bisectors of internal angles meet.

Therefore, MC is the angle bisector of angle AMD.

and m∠AMC ≅ m∠DMC

3x + 6 = 8x - 49

8x - 3x = 49 + 6

5x = 55

x = 11

b). m∠DMC = 8x - 49

= (8 × 11) - 49

= 88 - 49

= 39°

c). m∠MAD = 2(m∠DAC)

= 2(30)°

= 60°

d). Since, m∠AMD + m∠ADM + m∠MAD = 180°

2(39)° + m∠ADM + 66° = 180°

78° + m∠ADM + 66° = 180°

m∠ADM = 180° - 144°

= 36°

e). m∠ADC =
`(1)/(2)(m\angle ADM)`

=
`(1)/(2)(36)`

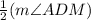
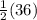
= 18°